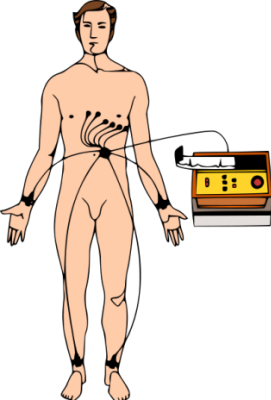
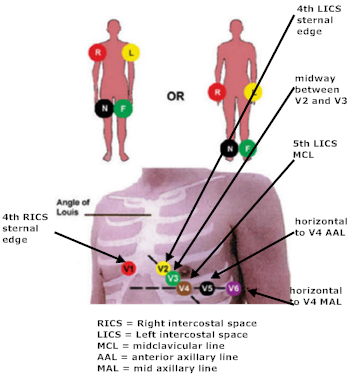
Understanding EKG

12 step approach to EKG interpretation
    Rate
    Rhythm
    Axis
    P wave
    PR interval
    PR segment
    QRS complex
    QRS amplitude
    QT interval
    ST segment
    T wave
    U wave

References

12 step approach to EKG interpretation

EKG strip

Rate

How to calculate the rate from first principles?

First find the speed of the EKG paper strip. It is normally set at 25 mm/s as shown above (bottom left). This means it traverses 25 mm in one second.

Let us practice some simple algebra:
If we get one QRS complex for every large box, this implies that you have 1 complex per 0.2 or 1/5 seconds or 5 complexes per 1 second or (5 x 60 = 300 complexes) per 60 seconds or 1 minute: => 300/min
If we get one QRS complex for every 2 large boxes, this implies that you have 1 complex per 0.4 or 2/5 seconds or 5/2 complexes per 1 second or (5/2 x 60 = 150 complexes) per 60 seconds or 1 minute: => 150/min
If we get one QRS complex for every 3 large boxes, this implies that you have 1 complex per 0.6 or 3/5 seconds or 5/3 complexes per 1 second or (5/3 x 60 = 100 complexes) per 60 seconds or 1 minute: => 100/min
If we get one QRS complex for every 4 large boxes, this implies that you have 1 complex per 0.8 or 4/5 seconds or 5/4 complexes per 1 second or (5/4 x 60 = 75 complexes) per 60 seconds or 1 minute: => 75/min
If we get one QRS complex for every 5 large boxes, this implies that you have 1 complex per 1 or 5/5 seconds or 5/5 complexes per 1 second or (5/5 x 60 = 60 complexes) per 60 seconds or 1 minute: => 60/min
If we get one QRS complex for every 6 large boxes, this implies that you have 1 complex per 1.2 or 6/5 seconds or 5/6 complexes per 1 second or (5/6 x 60 = 60 complexes) per 60 seconds or 1 minute: =>50/min

As you can see, there is a pattern: To find the rate you divide the number of boxes into 300 = 300/(# of large boxes)

If the pattern is regular in rhythm (see below), you can apply the above formula to get the rate. If the distance between the complexes is not a whole number of large boxes, then you can approximate it by dividing 300 into the fraction (e.g. 300/2.5 = 120).

From the strip above, it is a little less than 3 large boxes, so we know the rate is a little higher than 100/min.

If the pattern is irregular, the above rule cannot be used.
If you glance at the EKG strip above, you will see I have marked off the strip for every 5 large boxes or 1 second intervals, and as you can see, a strip runs for 10 seconds.
To calculate the rate, you count the number of complexes in the 10 seconds and then multiply by 6 to get the number of complexes in 60 seconds or 1 minute to get the average heart rate.
This can also be done even if the rhythm is regular.

For the strip above, there are 18 complexes in the rhythm strip (the lowest continuous reading above), so there are 18 x 6 = 108/min, which is what was expected.

Rhythm

Once you have calculated the rate, we can now determine the rhythm.

First determine if there is a P wave before each QRS complex. If there is a P wave before each complex, then the patient is said to be in sinus rhythm as the sinoatrial node is setting the pace for the heart and hence the rhythm.

If the rate calculated above is between 60 and 100, the patient is said to be in NORMAL SINUS RHYTHM.
If the rate calculated above is less than 60 the patient is said to be in SINUS BRADYCARDIA.
If the rate calculated above is greater than 100, the patient is said to be in SINUS TACHYCARDIA.

If there is no P wave before each QRS complex and the patient has an irregularly irregular rhythm, the patient is said to have ATRIAL FIBRILLATION.

If there are multiple P waves in a saw tooth pattern, or one P wave per each large box, then the patient is said to have ATRIAL FLUTTER.

Axis

The axis is the direction of the resultant summation of forces as the ventricles contract. To determine this, we use the principle that any vector can be resolved into 2 perpendicular components, and vice versa. That is if we have 2 perpendicular components of a vector, we know the direction of the resultant vector.

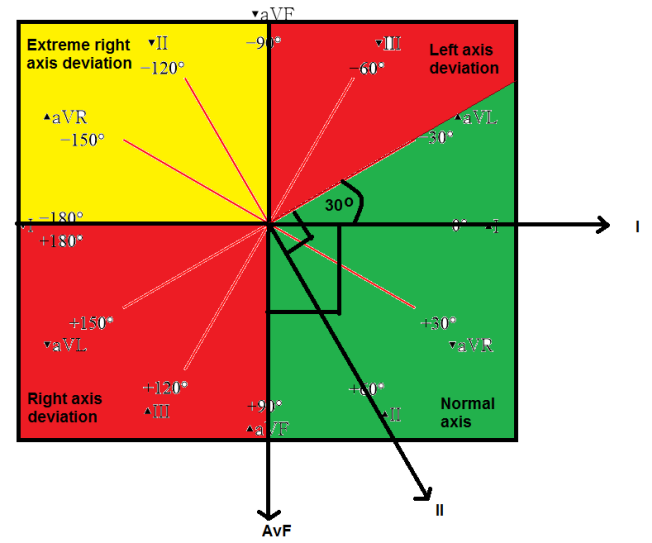
Axis of the heart

From above, the two perpendicular axes that would be used are I and AvF.

If I and AvF both have a net positive amplitude, then the axis is between 0 - 90 degrees, and hence is said to have normal axis.

If I has a net positive amplitude and aVF has a net negative amplitude, then the net deflection would lie between 0 and 90 degrees.

To determine if it is less than -30 degrees (green area above in the left upper quadrant) or more than - 30 degrees (the red area above in the left upper quadrant), we need to look at a lead that is perpindicular to the -30 degress line, and lead II fits the bill.

So we now turn to lead II, and if it is net positive, then the axis is less than -30 degrees (green), and hence normal axis. If is net negative, then it is more than -30 degrees (red), and hence the patient is said to have left axis deviation.

The other leads are straightforward.

If lead I is net negative, and lead AvF is net positive, then the patient is said to have right axis deviation.

If lead I is net negative and lead AvF is net negative, then the patient is said to have extreme right axis deviation.

The importance of knowing the axis of the heart, is that abnormal deviation of the resultant voltages are seen in certain heart conditions and may provide clues to underlying heart abnormalities.

This is summarised in the table below:

Axis	Lead I	Lead AvF	Lead II	Differential Diagnoses
Normal	+ve	+ve		Normal ( 0 - 90 degress)
Normal	+ve	-ve	+ve	Normal (-30 - 0 degrees)
Left axis deviation	+ve	-ve	-ve	Left ventricular hypertrophy Left bundle branch block Left anterior fascicular block
Right axis deviation	-ve	+ve		Right ventricular hypertrophy Right bundle branch block
Extreme right axis	-ve	-ve		Dextrocardia Reversal of leads

References

http://en.wikipedia.org/wiki/Electrocardiography
http://medictests.com/ecgcheatsheet/
http://www.bem.fi/book/15/15.htm